Surrogate Metrics for Infrastructure-Based Perception Evaluation
A structured approach for quantifying sensor effectiveness in infrastructure-based perception.
Overview
To systematically evaluate the effectiveness of infrastructure-based multi-modal sensor placement, we introduce surrogate metrics that quantify sensor perception performance. These metrics enable a structured assessment of different sensor configurations across diverse environmental conditions.
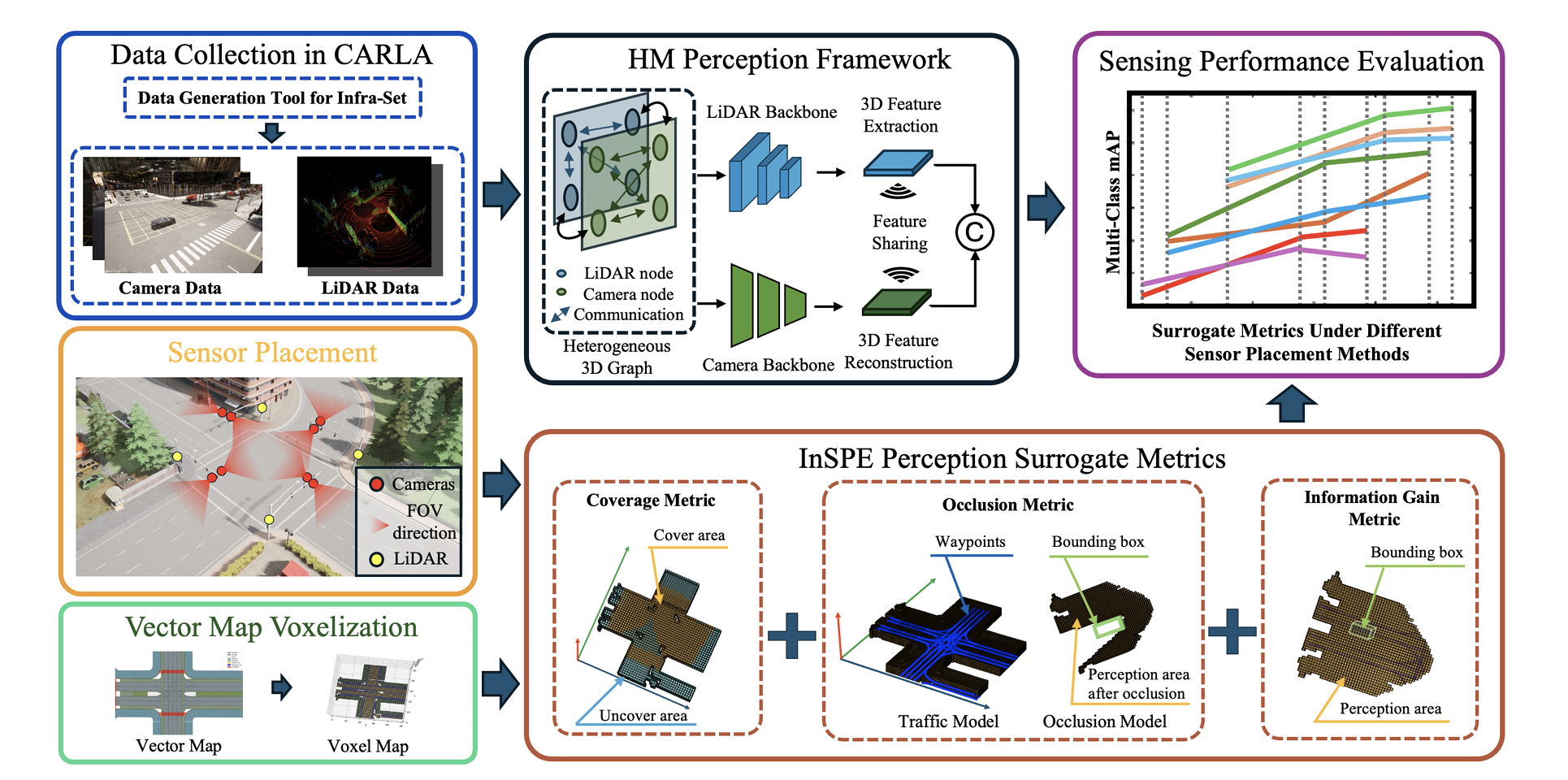
InSPE framework.
This page details the design of perception coverage, perception occlusion, and information gain metrics, which serve as key performance indicators in infrastructure-based perception evaluation. For more details on the implementation and benchmarking framework, see Simulation & Benchmarking for Infrastructure-Based Sensor Placement.
Camera and LiDAR Sensing Modeling
To evaluate the sensing capability of multi-modal sensor placements at intersections, we introduce a ray-cast sensing model for camera and LiDAR. This approach builds upon prior work and employs the Bresenham algorithm to efficiently compute the sensor’s view frustum or sensing range under a given placement \($ P_0\)$:
\[\Omega | P_0 = \{V_1^{P_0},V_2^{P_0},...,V_n^{P_0}, n \in N\}\]Camera Sensing Model
We model the camera’s field of view (FoV) as a frustum using the pinhole camera model. Each pixel in the image corresponds to a ray projection model, linking real-world coordinates \($ P(p_x, p_y, p_z)\)$, the image pixel \($ p(h_i, w_j)\)$, and the camera principal point \($ O^C(c_x, c_y)\)$.
The camera ray equation is defined as:
\[r_{ij}^{C}(\mu) = O^C + \mu \cdot d_{ij} = O^C + \mu \cdot \begin{bmatrix} (w_{j} - c_x)/f \\ (h_{i} - c_y)/f \\ 1 \end{bmatrix}\]where \($ \mu \geq 0\)$, and \($ d_{ij}\)$ is the ray direction.
LiDAR Sensing Model
LiDAR sensing is modeled using discrete beam emission, where each beam is a ray emanating from the LiDAR origin \($ O^L\)$, with direction defined by horizontal scanning angle \($ \theta^L\)$ and vertical scanning angle \($ \psi^L\)$:
\[r^{L}_{ij}(t) = O^L + t\cdot d_{ij} = O^L + t \begin{bmatrix} \cos\psi^L_{i} \cos\theta^L_{j} \\ \cos\psi^L_{i} \sin\theta^L_{j} \\ \sin\psi^L_{i} \end{bmatrix}\]where \($ 0 \le t \le t_{\max}\)$.
Surrogate Metric Design
Perception Coverage Metric
We define a perception coverage metric \($ C\)$ to quantify the effective sensing region of sensors in an intersection. Using the ray-cast sensor model:
\[f(V_i) = \begin{cases} 1, & \text{if sensor ray passes through } V_i, \\ 0, & \text{otherwise} \end{cases}\]The weighted perception coverage is computed as:
\[C = \frac{\sum_{V_i \in \Omega} w(V_i) \cdot f(V_i)}{\sum_{V_i \in \Omega} w(V_i)}\]where \($ w(V_i)\)$ represents importance weights assigned to different intersection regions, following safety prioritization.
Perception Occlusion Metric
To measure the occlusion effect caused by objects (e.g., vehicles, pedestrians), we introduce an occlusion probability metric \($ O\)$. This metric integrates a waypoint-based bounding box traffic model, defining occluded regions based on vehicle positions and trajectories.
The occlusion ratio for a given waypoint frame \($ k\)$ is:
\[O^{(k)} = \frac{|V_{\text{occ}}^{(k)}|}{|V_{\text{orig}}^{(k)}|}\]where \($ V_{\text{orig}}^{(k)}\)$ represents the original visible region, and \($ V_{\text{occ}}^{(k)}\)$ is the occluded subset. The total occlusion probability is then computed as:
\[O = \frac{1}{N} \sum_{k=1}^{N} 1 - \frac{|V_{\text{occ}}^{(k)}|}{|V_{\text{orig}}^{(k)}|}\]Comparison with Benchmarking Models
To validate the effectiveness of our surrogate metrics, we compared them with multi-class mAP results from several benchmarking models. The results, shown in Figure 4, demonstrate a strong positive correlation between perception surrogate metrics and multi-class detection performance.
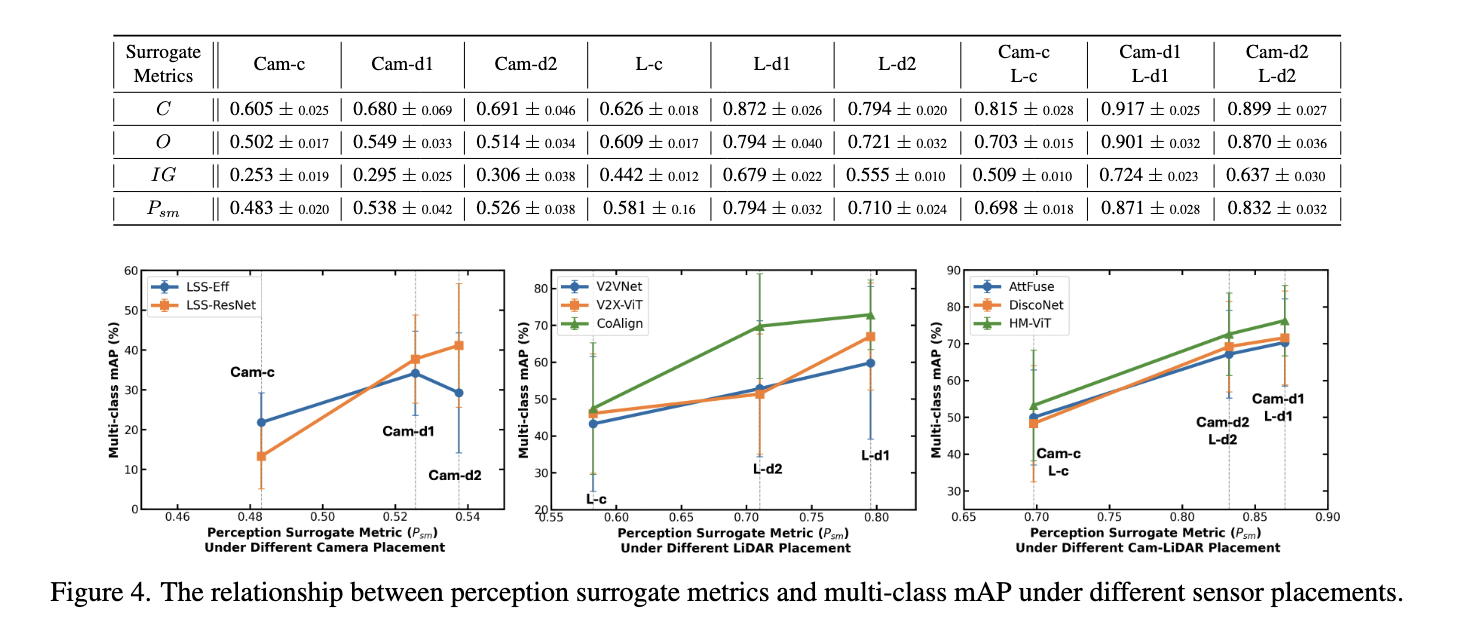
Figure 4. Relationship between perception surrogate metrics and multi-class mAP under different sensor placements.
- Higher perception coverage (C) and lower occlusion (O) values lead to improved mAP across different sensor placements.
- LiDAR-enhanced placements outperform camera-only setups in multi-class detection.
- Hybrid camera-LiDAR configurations provide the most robust perception across all sensor placements.
These findings confirm that our surrogate metrics align well with real-world perception performance, making them valuable for optimizing sensor deployments in infrastructure-based perception systems.
Summary
This page introduces the design of surrogate metrics for infrastructure-based perception evaluation, focusing on:
- Perception Coverage: Measuring sensor effectiveness in different spatial regions.
- Perception Occlusion: Capturing occlusion effects caused by dynamic objects.
These metrics provide a structured approach for assessing sensor placement strategies. The benchmarking results validate that higher perception surrogate scores correspond to improved object detection accuracy.
For a full evaluation of benchmarking experiments and sensor placement strategies, refer to Simulation & Benchmarking for Infrastructure-Based Sensor Placement.